二叉树的数据结构以及其相关特性整理
树相关知识
结点概念
结点是数据结构中的基础, 是构成复杂数据结构的基本组成单位, 本文中的节点只树节点, 为一个数据单元
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
名词解释:
树: N个有父子关系的节点的有限集合, 与堆, 栈, 队列不同, 树是一种非线性的集合
1)有且仅有一个特定的称为根(Root)的结点;
2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1、T2、......、Tn,其中每一个集合本身又是一棵树,并且称为根的子树。
节点: 组成树的每个元素点为节点, 通常包含一个 [数据包] 以及 [若干指针] 指向其他节点
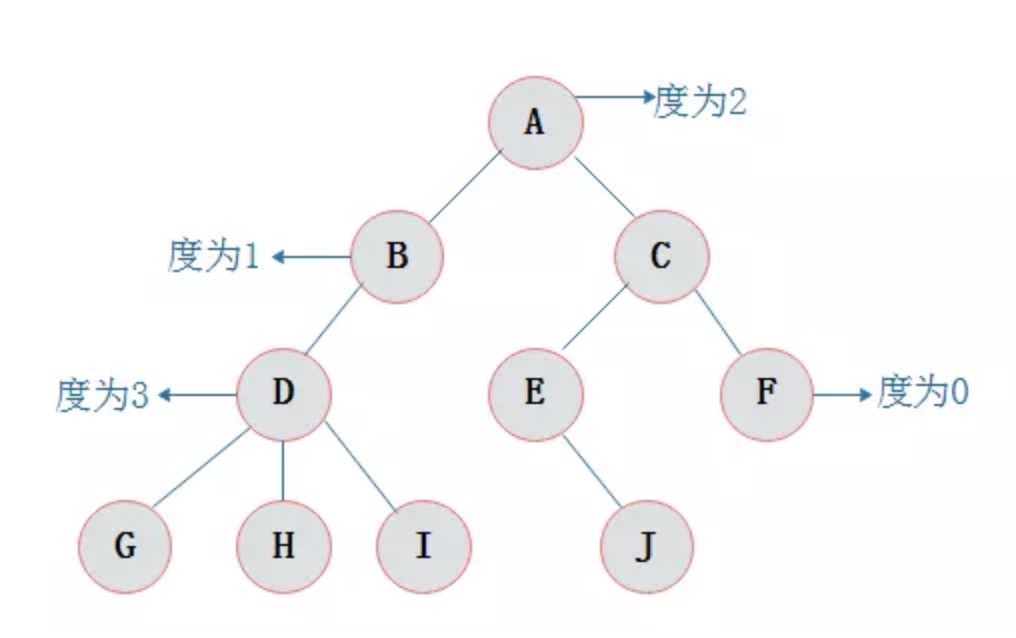
度(节点): 节点拥有的子树的数量叫做节点的度
度(树): 所有节点的度的和为树的度
子节点: 当前节点 子树 的 根节点 为当前节点的子节点
父节点: 参照 [子节点] , 拥有子节点的当前节点为子节点的父节点
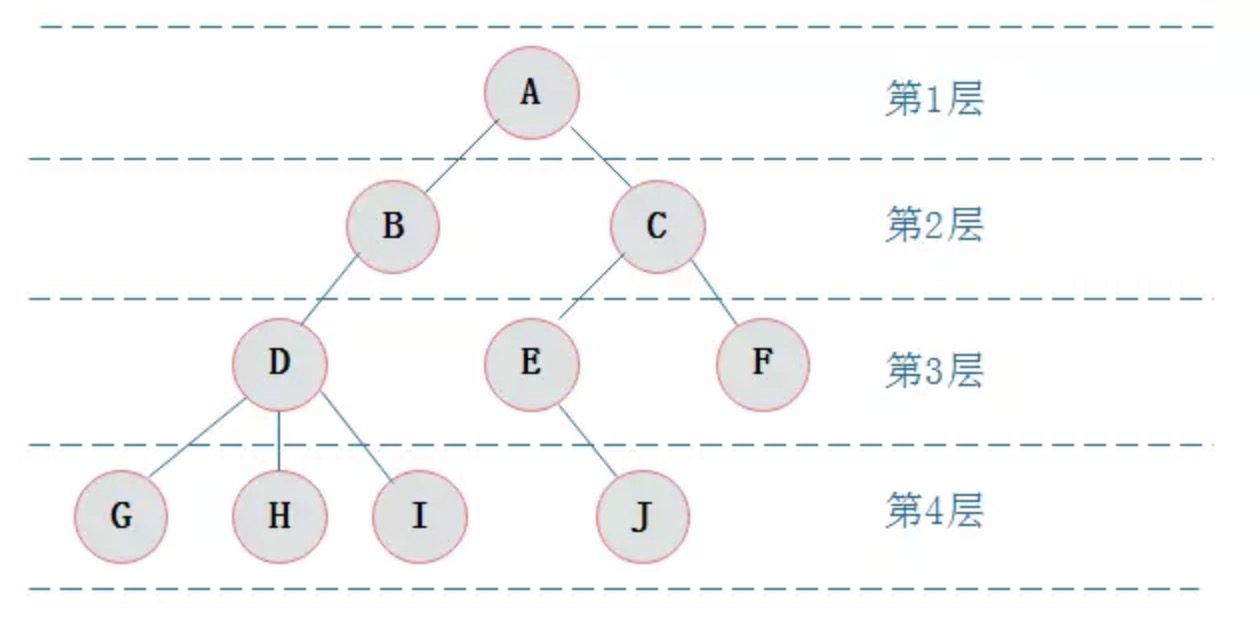
层次(level): 从根节点算起, 根节点为1, 其余节点的层次为当前节点的父节点+1
深度(depth): 最大层次为深度
祖先节点: 从根节点到当前节点经过的所有节点
后代节点: 以当前节点为根节点的子树包含的所有节点为当前节点的后代节点
1
2
3
4
树的特性:
1.任意非空的树有且仅有一个根节点
2.一棵树由 根 和 若干个子树 组成, 每个子树也可有由若干个子树组成
1
2
3
4
5
6
7
8
节点的分类:
1.以父节点为参照:
有父节点: 普通节点
无父节点: 根节点
2.以子节点为参照:
有子节点: 普通节点
无子节点: 叶子节点
二叉树:
二叉树定义:
从根节点开始, 每个节点最多拥有两个子节点的有序树
二叉树的特性:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
分左右树, 左边的子树为[左子树], 右侧为[右子树]
节点最大的 度 为2 -> 最多有两个子树 [子节点]
一颗二叉树如果包含了2^K - 1 个节点 [k为当前树深度] , 当前树为 [满二叉树]
一颗 深度为K 的二叉树, 按每层从左到右依次编号, 若此二叉树的编号 与 深度同样为K的满二叉树以同样的规则的编号完全一致, 当前树为完全二叉树
二叉树第i层上的节点数据至多为2的i-1次方
具有n个节点的满二叉树的深度为log2 (n+1)
深度为k的二叉树至多有2的k次方-1个节点.满二叉树的每层节点的数量依次为1, 2, 4, 8,…,因此深度为k的满二叉树包含的节点数为公比为2的等比数列的前k项总和,即2的k次方一1。
在任何一棵二叉树中,如果其叶子节点的数量为x, 度为2的子节点数量为y,则x=y + 1。这是因为:如果为任意叶子节点增加一个子节点,则原有叶子节点变成非叶子节点,新增节点变成叶子节点,上述等式不变;如果为任意叶子节点增加两个子节点,则原有叶子节点变成度为2的非叶子lto点,新增的两个节点变成叶子节点,上述等式依然不变。
满二叉树
在一棵二叉树中。如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。
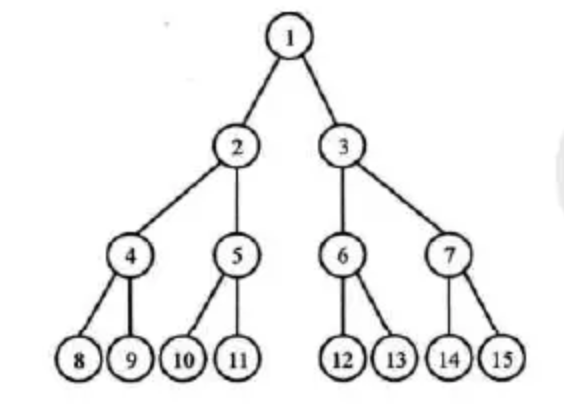
满二叉树
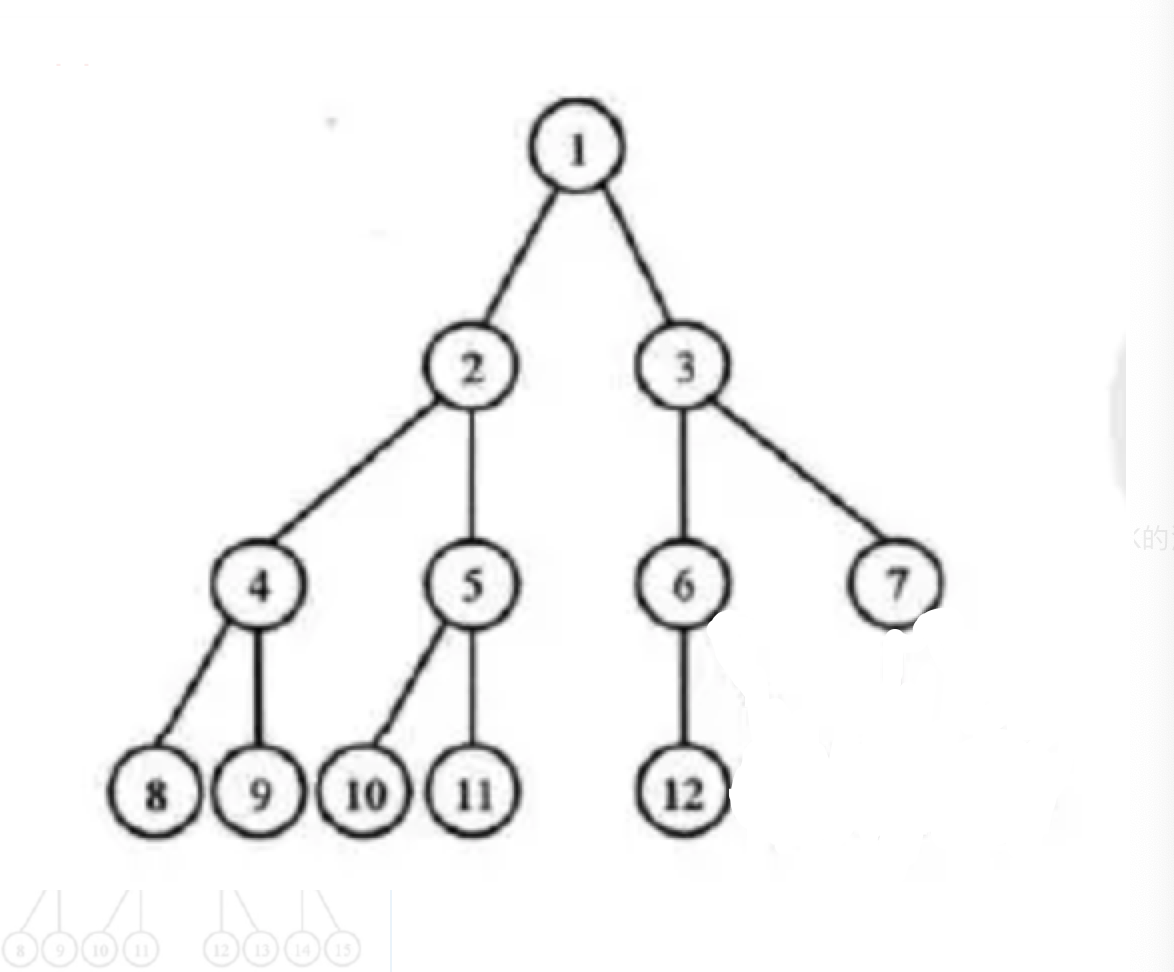
完全二叉树
对于一颗具有n个节点的完全二叉树的节点按层自左向右编号,则对任一编号为i(n>=i>=1)的节点有下列性质:
1
2
3
4
5
6
7
当i==1时,节点i是二叉树的根;若i>1,则节点的父节点是i/2
若2i<n,则节点i有左子节点,左子节点的编号是2i;否则,节点无左子节点,并且是叶子节点
若2i+1<=n,则节点i有右子节点,右子节点的编号是2i+1;否则,节点无右子节点。
1~n/2范围的节点都是有子节点的非叶子节点,其余的节点全部都是叶子节点。编号为n/2的节点可能只有左子节点,也可能即有左子节点,又有右子节点。
对于数组实现的二叉树, 使用顺序存储可避免空间浪费, 即按每层从左至右存储, 但是如果存储的二叉树为不完全二叉树, 就会出现存储浪费, 所以二叉树的存储, 不推荐使用数组
二叉树的二叉链表的实现:
1
2
left point || val || right point
左侧子节点指针, 数据, 右侧子节点指针
遍历方式:
1
2
3
4
5
6
L为左子树 R为右子树 D为根节点
广度遍历: 按照规则, 按层遍历(层序遍历)
深度遍历: 按照一定的规则, 一直向下遍历
先序遍历: DLR
中序遍历: LDR
后序遍历: LRD
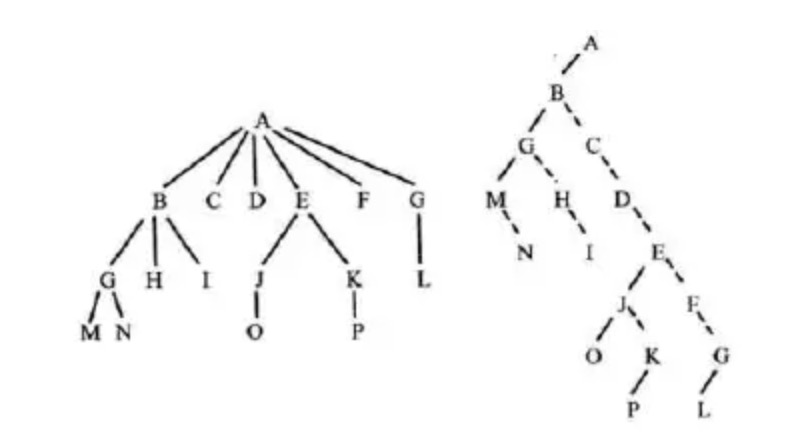
多叉树转二叉树:
1
2
3
加虚线: 同一个父节点的相邻兄弟节点之间加虚线
抹实线: 每个节点只保留它与最左子节点的连线,与其他字节点的连线都被抹掉。
虚改实: 虚线改为实线
二叉查找树
1
2
3
4
5
6
二叉查找树,也称有序二叉树(ordered binary tree),或已排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
若任意节点的左子树不空, 则左子树上所有结点的值均小于它的根结点的值
若任意节点的右子树不空, 则右子树上所有结点的值均大于它的根结点的值
任意节点的左、右子树也分别为二叉查找树
没有键值相等的节点(no duplicate nodes)
红黑树
1
2
3
算法导论对R-B Tree的介绍:
红黑树,一种二叉查找树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。
通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
结束语:
通过以上文章的阅读, 可以初步掌握二叉树的基本原理以及相关特性, 在实际的开发应用当中, 二叉树的身影随处可见(collection, memory cache, database), 它被包装了一层语法糖, 我们要善于发现并掌握其中原理, 这样在提升自己的同时, 还可以极大的提高程序的运行效率, 关于红黑树, B树等比高级的算法, 留待以后继续钻研讨论